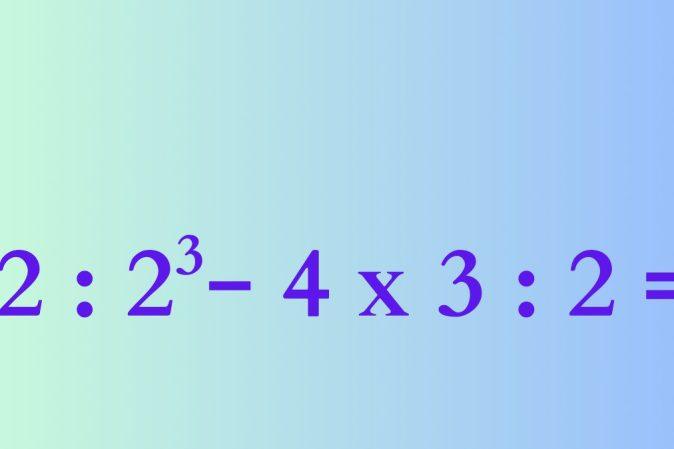Pateiktą pavyzdį galima išspręsti vos per kelias sekundes net nenaudojant skaičiuotuvo. Vis dėlto būtina būti atidiems ir nepatekti į spąstus, kurie laukia tų, kurie skuba arba pamiršta pagrindines matematikos taisykles. Toliau paaiškiname, kaip teisingai išspręsti šį veiksmą ir koks yra jo rezultatas.
Žiūrint į ilgesnius, sudėtingesnius matematinius veiksmus, kuriuose pasirodo keli skirtingi simboliai, nesunku pasijusti pasimetus ir nebežinoti, nuo ko pradėti. Tokiu atveju neverta skubėti ar visko skaičiuoti mechaniškai iš kairės į dešinę, verčiau prisiminti vieną svarbią taisyklę iš pradinės mokyklos.
Žinoma, kalbame apie veiksmų atlikimo eilės taisyklę. Pagal ją pirmiausia atliekami veiksmai skliausteliuose, tuomet – laipsniavimas ir šaknijimas. Po to atliekame daugybą ir dalybą, vykdomas nuosekliai iš kairės į dešinę.
Tik pačioje pabaigoje pereiname prie sudėties ir atimties – tai veiksmai, turintys žemiausią prioritetą ir taip pat atliekami iš kairės į dešinę. Laikantis šios paprastos taisyklės, pateiktą veiksmą galima išspręsti vos per kelias akimirkas ir be klaidų.
Kaip išspręsti pavyzdį, taikant veiksmų atlikimo eilę?
Veiksmų sprendimas gali atrodyti sudėtingas, jei žiūrime į visą išraišką kaip į vieną visumą. Verčiau ją suskaidyti į mažesnes dalis, griežtai laikantis veiksmų atlikimo eilės. Taip kiekvienas žingsnis tampa aiškus, o visas uždavinys – daug paprastesnis.
Žemiau paaiškiname, kaip žingsnis po žingsnio apskaičiuoti veiksmą: 72 : 2³ − 4 × 3 : 2. Štai ką reikia daryti:
- Pirmiausia apskaičiuojame laipsnį, esantį išraiškoje: 2³ = 8.
- Tada atliekame pirmąją dalybą: 72 : 8 = 9.
- Kitame žingsnyje atliekame daugybą: 4 × 3 = 12.
- Po daugybos apskaičiuojame gauto rezultato dalybą: 12 : 2 = 6.
- Galiausiai atliekame paskutinį veiksmą: 9 − 6.
Atlikus visus žingsnius, gauname teisingą rezultatą – tai yra 3. Tiksli veiksmų atlikimo eilės laikysena leidžia šį pavyzdį išspręsti akimirksniu ir be klaidų.